Regresja – definicja, zastosowanie, przykłady

Termin regresja wywodzi się z języka łacińskiego i oznacza cofanie. Po raz pierwszy użyty został w 1885 roku przez Francisa Galtona – brytyjskiego naukowca, lekarza, antropologa
i statystyka, ucznia Karola Darwina. Galton prowadził badania nad istnieniem zależności pomiędzy wzrostem rodziców a wzrostem dzieci. Przeprowadzone przez niego badanie udowodniło, iż potomstwo osób o ponadprzeciętnym wzroście, cechuje się niższym wzrostem. Z kolei rodzice posiadający wzrost znacznie niższy od średniego zwykle posiadają dzieci z wyższym wzrostem. Francis Galton zaobserwowane zjawisko nazwał cofaniem w kierunku przeciętności.

Regresja liniowa jest metodą służącą do opisu zależności zachodzących między zmienną objaśnianą (niezależną) oraz jedną bądź wieloma zmiennymi zależnymi, mającymi charakter liczbowy. Analiza regresji stosowana jest jak narzędzie badawcze. Dzięki niej możliwe jest bowiem opisanie oraz zrozumienie wielowymiarowych zjawisk.

Dodatkowo znajduje ona szerokie zastosowanie w procesie predykcji (prognozowania). Zastosowanie regresji liniowej pozwala stwierdzić, o ile średnio wzrośnie wartość zmiennej objaśnianej w sytuacji oraz kiedy wartość zmiennej objaśniającej wzrośnie o jednostkę. Krzywa regresji liniowej wykazywać może dodatnią bądź ujemną zależność liniową.

Aby ocenić dokładność dopasowania modelu do danych empirycznych można posłużyć się:

1. Współczynnikiem determinacji (R²) – informuje o tym, jaka część zmienności zmiennej zależnej (objaśnianej) została wyjaśniona przez zmienne niezależne (objaśniające). Jego wartość mieści się w przedziale [0;1], zaś im jest ona bliższa 1, tym lepsze jest dopasowanie funkcji regresji do danych empirycznych.
2. Współczynnik zbieżności – określa, jaka część zmienności zjawiska nie została wyjaśniona przez zmienne niezależne. Jego wartość mieści się w przedziale [0;1], zaś im jest ona bliższa 0, tym lepsze jest dopasowanie funkcji regresji do danych empirycznych.
3. Odchyleniem standardowym (https://obliczeniastatystyczne.pl/odchylenie-standardowe/) składnika resztowego – informuje nas, o ile, średnio wartości empiryczne zmiennej zależnej odchylają się od jej wartości teoretycznych (czyli tych, które wyliczone zostały przy zastosowaniu funkcji regresji liniowej).
4. Współczynnikiem zmienności (https://obliczeniastatystyczne.pl/wspolczynnik-zmiennosci) resztowej – wskazuje, jaki procent średniego poziomu zmiennej zależnej stanowi odchylenie standardowe składnika resztowego. Innymi słowy, określa on jaką część średniej wartości zmiennej zależnej stanowią wahania losowe.

Regresja liniowa wzory

Wzór na równanie regresji liniowej (1):

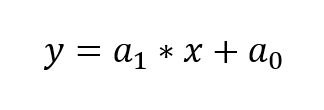
Gdzie:

a₁ oznacza – współczynnik kierunkowy

a₀ – wyraz resztowy (wolny)

Równie często spotykamy także inne warianty tego wzoru

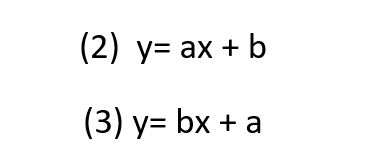
Symbol znajdujący się przy zmiennej niezależnej x zawsze będzie oznaczać współczynnik kierunkowy, a symbol znajdujący się po znaku „+” odpowiednio – składnik resztkowy. Już sama postać wzoru wyraźnie wskazuje na to,
że mamy do czynienia z funkcją liniową.

Powracając do pierwszego wzoru, wyznaczenie parametrów a i b możliwe jest dzięki zastosowaniu poniższych wzorów:

Przykład:

W celu prawidłowego zrozumienia istoty regresji liniowej warto posłużyć się przykładem.
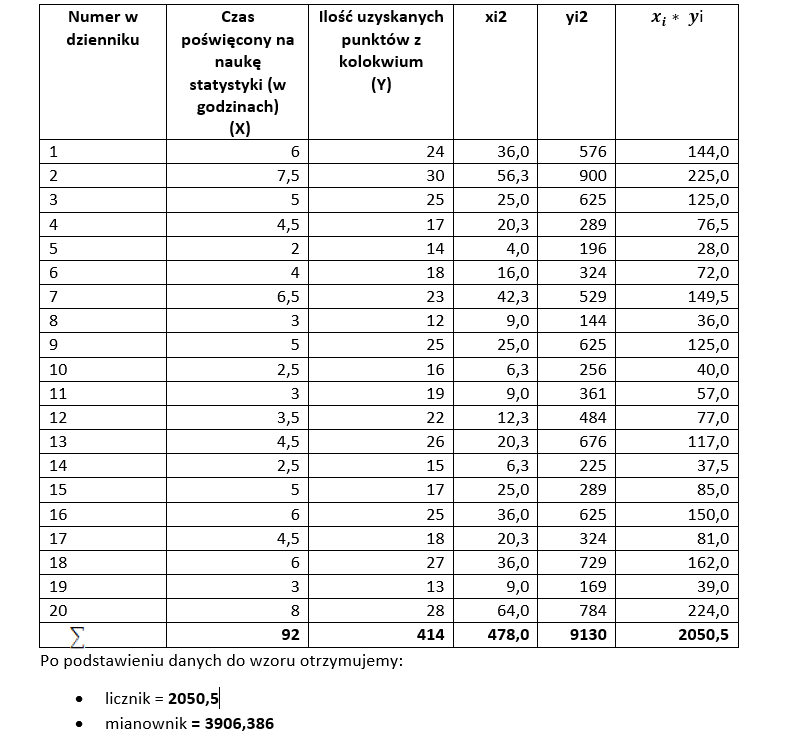
W poniższej tabeli zestawiono ze sobą liczbę punktów uzyskaną przez poszczególnych studentów z kolokwium oraz czas poświęcony na naukę statystyki. Korzystając z przedstawionych wyżej wzorów możemy obliczyć parametry a­₁ oraz a₀.

Wyznaczanie a­₁

Zatem:
  a­₁ wynosi 0,261,

a₀ wynosi 4,339,

Równanie funkcji regresji będzie miało zatem postać:

Y= 0,261x + 4,389

Poza równaniem regresji konieczne jest także wyliczenie:

• współczynnika korelacji R Pearsona
• współczynnika determinacji R²
• współczynnika zbieżności φ2= 1 – R²
• istotności statystycznej (na podstawie rozkładu teoretycznego F Snedecora bądź
  T-Sudenta)

Współczynnik korelacji określa związek pomiędzy dwiema zmiennymi lub pomiędzy jedną zmienną
a połączeniem wielu zmiennych (tzw. korelacja wielozmienne/wieloraka).

Współczynnik korelacji parametrycznej  R Pearsona wskazuje jednocześnie  na siłę związku (oscylującą pomiędzy wartościami bezwzględnymi od 0 do 1) oraz na kierunek związku. Rozróżniamy zatem korelacje:

• brak korelacji – o wartości bezwzględnej mniejszej bądź równej 0,2
• słabe – od 0,2 do 0,4
• umiarkowane – od 0,4 do 0,7
• silne – od 0,9 do 0,9
• bardzo silne pow. 0.9

Jakie mogą być kierunki korelacji?

Kierunek korelacji może być:

• ujemny/negatywny (kiedy wraz ze wzrostem wartości jednej zmiennej wartości drugiej zmiennej maleją)
• dodatni/ pozytywny (kiedy wraz ze wzrostem wartości jednej zmiennej wartości drugiej zmiennej wzrastają).

Nieodzownym czynnikiem w przypadku korelacji jest logiczny związek pomiędzy zmiennymi. Korelacje bez takiego związku nazywamy pozornymi.

Wzór na korelację R Pearsona

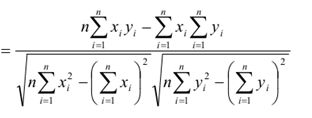
W omawianym przykładzie siła korelacji wyniosła 0,83 (korelacja dodatnia silna)

Współczynnik determinacji R² to odsetek danych, które odzwierciedlają prostą regresji.

• W omawianym przykładzie współczynnik determinacji wyniósł 0,63 (63%).
• Wartość test F Snedecora wyniosła 37,72
• Istotność wyniosła 0,001

Wnioski z podanego przykładu:

1. Istnieje zależność pomiędzy czasem poświęconym na naukę o oceną (korelacja jest silna i dodatnia).
2. Im dłuższy czas nauki, tym lepsze wyniki egzaminu
3. Współczynnik determinacji wyniósł 63%, co oznacza że na w 37% (na podstawie współczynnika zbieżności) na wyniki egzaminu wpłynęły inne czynniki niż czas nauki.

Wykorzystanie rachunku regresji do predykcji i ekstrapolacji trendów      

Uzyskane równanie liniowe regresji pozwala na w miarę dokładne oszacowanie wartości zmiennej, a nawet na tzw. ekstrapolację trendu czyli przeniesienie trendów na przyszłość. Oczywiści, ekstrapolacja obarczona jest bledem wynikającym z tego, że:

• trendy nie zawsze są liniowe,
• nie zawsze działają a jednakowa dynamiką,
• istnieje wiele czynników zewnętrznych, które mogą wpłynąć na wartość trendu.

Ogólne równanie regresji opisujące trend ma postać

Y= tx + b

Gdzie t oznacza konkretną jednostkę czasową (x=0 to pierwszy zbadany element)

Jak powinna być przeprowadzona regresja liniowa w Excel?

Korzystając z Excela posiadamy wiele możliwości obliczenia równania regresji liniowej
w Excelu. Jednym ze sposobów obliczenia parametrów regresji liniowej jest podstawienie wszystkich potrzebnych danych do wzoru. Excel znacznie ułatwia nam to zadanie. Posługując się podanym wyżej przykładem w poniższej tabeli przedstawione zostały wszelkie wyliczenia niezbędne do analizy regresji liniowej. Oczywiście warto pamiętać także,
że w większości programów statystycznych możemy także wykonać regresję.

Wiele szczegółowych obliczeń możemy uzyskać poprzez zastosowanie odpowiednich funkcji statystycznych Excela (wykorzystanie funkcji f(x)). Są to m.in.:

• Średnia,
• Wariancja,
• Błąd oszacowania,
• Korelacja Perasona R,
• Determinacja R².

W ten sposób bez problemu policzymy regresję i wszystkie jej elementy składowe.        

• Ponadto Excel daje nam możliwość znacznie szybszego obliczenia parametrów równania regresji liniowej.
• Możemy wreszcie na wykresie uzyskać dokładne równanie i współczynnik determinacji.
• Najlepszym rozwiązaniem jest skorzystanie z dodatku do Excela Analysis ToolPak

Interpretacja:

• df – stopnie swobody
• SS – odchylenie wartości obserwowanych od oczekiwanych
• MS – dokładne oszacowanie odchylenia (uwzględniające wartości średnie
• Istotność F – poziom istotności p (w analizowanym przykładzie pierwsze cyfry różne od 0 znajdują się na piątym miejscu po przecinku, a przyjęty krytyczny poziom istotności wynosi  p</= 0,05.

Wyznaczanie równania trendu na podstawie analizy regresji liniowej przy pomocy Excela

Procedura w Excelu 2013-2020 polega na:

• zaznaczeniu maksymalnie dwóch zmiennych,
• dodaniu linii trendu i wykorzystaniu opcji .

Przykład:

Porządkujemy dane, tak by zmienna X (nasz t) utworzyła szereg prosty (od wartości najmniejszej do największej).

Sporządzamy wykres (najlepiej punktowy)

• Zaznaczamy dowolny punkt (wartość) na wykresie (prawym przyciskiem myszki)
  i wybieramy opcje linia trendu.
• Wybieramy: Rodzaj Trendu (w naszym wypadku liniowy) wybieramy  Przecięcie, Równanie na wykresie i R².
• Wybieramy Prognozę (np. 2 okresy do przodu).

Mając 17 danych podstawowych (w tym rok „0”) możemy przewidzieć wartości trendu w kolejnych latach:

• Za rok 2022 podstawiamy kolejną wartość (18),
• Za rok 2023 podstawiamy kolejną wartość (19),

Podstawiamy do wzoru i otrzymujemy oszacowanie trendu.

• Jeżeli chcemy określić wartość np. za I kwartał 2006 roku (podstawiamy X o wartości 2,25.

Regresja liniowa z wieloma zmiennymi zależnymi

W praktyce na wartość zmiennej zależnej często wywierają wpływ liczne zmienne niezależne. Dlatego też warto przybliżyć inny przykład, który pokaże nam jak można wykorzystać analizę regresji liniowej.

W poniższej tabeli zestawiono ze sobą przeciętny dochód rozporządzalny na 1 osobę, przeciętne wydatki na gastronomię oraz przychody z działalności gastronomicznej w latach 2005-2020. Zakładając, iż średni rozporządzalny dochód w 2021 roku wyniesie 2097,15 zł, zaś średnie wydatki na gastronomię wzrosną do 80,5 zł możliwe będzie oszacowanie tego, jak zmienią się przychody z działalności gastronomicznej w Polsce. Ten przykład w przystępny sposób zobrazuje jaki potencjał ma regresja liniowa.

• Wykorzystujemy Analysis ToolPak, który został umieszczony w menu: Dane.
• Wybieramy zmienną niezależną i zmienne zależne.
• Wykonujemy polecenie z menu Dane – Regresja

Przykład

Uzyskujemy następujący zestaw tabel

Następnie analizujemy tabele obserwacji teoretycznych i sprawdzamy przy tym czy odchylenia składników resztkowych w każdej z analizowanych obserwacji mieści się co najmniej w obszarze pomiędzy tzw. wartością graniczną (2 odchylenia składników resztkowych) i wartością odrzucenia (3 odchylenia składników resztowych)

• Jeżeli, którakolwiek obserwacja przekracza tę wartość, to usuwamy ją z danych wyjściowych i obliczmy całość ponownie.

Obserwacja	Przewidywane 761,46	Składniki resztowe	Standaryzowane składniki resztkowe
1	936,739	-102,059	-2,14259
2	992,4203	-63,5503	-1,33415
3	1046,36	-0,84028	-0,01764
4	1098,064	16,13632	0,338759
5	1140,295	52,52533	1,102696
6	1168,93	58,02031	1,218055
7	1213,025	65,40517	1,37309
8	1251,088	47,98188	1,007312
9	1308,697	31,74348	0,66641
10	1397,723	-11,5626	-0,24274
11	1525,754	-51,1942	-1,07475
12	1614,211	-16,0809	-0,3376
13	1686,863	6,59662	0,138487
14	1857,889	-38,7486	-0,81347
15	1938,898	-19,8984	-0,41774
16	2071,625	25,52512	0,535864

W naszym przypadku wszystkie obserwacje zostały przyjęte.

Przechodzimy zatem do analizy wariancji

• p</= 0,001
• p</= 0,01
• p</= 0,05

Przyjmujemy hipotezę roboczą zakładającą współzależność pomiędzy zmiennymi zależnymi.

	Współczynniki	Błąd standardowy	t Stat	Wartość-p
Test T-Studenta	591,6834	41,47945	14,26449	0,001

Dla uszczegółowienia interpretacji obliczmy macierz korelacji ponownie korzystając z Analysis ToolPak.

• W menu Dane wybieramy Korelacja.
• Zaznaczamy wszystkie wartości zmiennej Y i zmiennych X.

Wynik analizy korelacyjnej wskazuje na nieznacznie silniejszy związek zmiennych  Przeciętny dochód rozporządzalny na 1 osobę PLN  oraz Przychody z działalności gastronomicznej PLN .

Wnioskowanie:

Zbadano współzależność pomiędzy zmienną: Przeciętny dochód rozporządzalny na 1 osobę PLN , a parą zmiennych:

• Przeciętne wydatki na gastronomię PLN
• Przychody z działalności gastronomicznej PLN
• Analiza regresji wielozmiennej wskazuje na istotny statystycznie związek pomiędzy badanymi zmiennymi.
• Nieznacznie silniejszy związek zaobserwowano pomiędzy zmiennymi: Przeciętne wydatki na gastronomię PLN  oraz Przychody z działalności gastronomicznej PLN.
• Przeciętny dochód rozporządzalny na 1 osobę PLN  koreluje statystycznie z Przeciętnymi wydatkami na gastronomię PLN  oraz Przychodami z działalności gastronomicznej PLN.
• W kolejnym roku dochody wzrosną do wartości prognozowanej  2071,62 PLN.

Wykorzystanie funkcji Reglinp a regresja

Innym sposobem na wykorzystanie Excela w wielozmiennej analizie wariancji liniowej jest skorzystanie z funkcji f(x): Reglinp 

Z uwagi na fakt, iż niektóre wersje Excela powodują błędy w obliczeniach tej funkcji przy wykorzystaniu Analysis ToolPak – najprościej wyznaczyć tę funkcję dla  pierwszej kolumny z danymi tabeli korzystając z funkcji F(x).

Po otrzymaniu pojedynczego wyniku zaznaczamy obszar liczący wszystkie kolumny oraz
5 wierszy używamy kombinacji klawiszy: Ctrs + Shift + Enter.

W tym obliczeniu nasza wcześniej uzyskana wartość powinna znajdować się w pierwszej kolumnie
i w pierwszy wierszu.

Po obliczeniu uzyskujemy uproszczoną macierz analizy regresji wielozmiennej.

Funkcja Reglinp   nie wyświetla na danych o istotności, lecz prezentuje dane o składnikach resztkowych. Jej zastosowanie nie jest zatem tak przydatne, jak analiza regresji z wykorzystaniem Analysis ToolPak.

Podstawowe informacje odnośnie pojęcia regresja liniowa można znaleźć także tutaj. Z kolei osobom poszukującym bardziej specjalistycznego opisu praktycznego zastosowania regresji polecamy artykuł przygotowany przez pana Janusza Wątrobę, dostępny na stronie firmy Statsoft, będącej dystrybutorem oprogramowania Statistica

Zdjęcie główne użyte w naszym artykule o regresji: Obraz autorstwa kroshka__nastya na Freepik