Dowiedz się czym dokładnie jest test chi kwadrat

Chi kwadrat – z pewnością zetknęliście się Państwo z tym pojęciem wielokrotnie, jednak osoby nie zajmujące się zagadnieniami statystycznymi na co dzień, z pewnością mogą mieć pewne trudności w prawidłowym zastosowaniu i interpretacji tego testu. W krótki i przystępny sposób wyjaśnimy zatem czym jest test chi kwadrat i w jakim celu się go stosuje.

Najprościej mówiąc  jest to grupa testów nieparametrycznych charakteryzującą  się tym, iż rozkład statystyki testowej przybiera rozkład chi kwadrat, jeśli teoretyczna zależność jest prawdziwa.

Chi kwadrat – zastosowanie 

Najczęstszym zastosowaniem testów chi kwadrat jest analiza wyników zebranych podczas badania ankietowego.
Bardzo ważną cechą testu chi kwadrat jest możliwość wykorzystywania go zarówno do mierzenia zależności cech mierzalnych jak i cech niemierzalnych. Możliwość zweryfikowania istotność w oparciu o zmienne niemierzalne powoduje, iż chi kwadrat jest jednym z najczęściej wykorzystywanym testów w praktyce.

Dodatkowym atutem testu jest fakt małej liczby założeń, wyróżnia się dwa podstawowe założenia jakie powinny zostać spełnione przed zastosowaniem testu:

• Niezależność grup co oznacza, że pomiar danej cechy dokonywany jest na obiektach należących do różnych grup ( obiekt nie może należeć jednocześnie do dwóch grup)
• Duże liczebności oczekiwane co oznacza, że żadna z liczebności oczekiwanych nie może być mniejsza niż 1 oraz nie więcej niż 20% liczebności oczekiwanej może być mniejsza od 5.

Dzięki „chi kwadrat” dokonujemy porównania wartości obserwowanej z wartościami oczekiwanymi. Wzór tego testu ma postać:

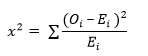
Gdzie:
O_ – wartość mierzona
E_ – wartość oczekiwana

 

 

Najczęściej używane są dwa podstawowe rodzaje testów:

I.  Test niezależności chi kwadrat

Wykorzystywany w celu sprawdzenia czy dwie zmienne są niezależne od siebie (brak korelacji). Odpowiada na pytanie czy związek między zmiennymi jest statystycznie istotny.

Przykładowy problem badawczy: Czy płeć badanych wpływa na ich skłonność do palenia papierosów?

II.  Test zgodności chi kwadrat

Wykorzystywany w celu sprawdzenia równoliczności grup oraz gdy dokonujemy porównania empirycznego rozkładu z rozkładem teoretycznym (założonym).

Przykładowy problem: Czy w badanej próbie pacjentów liczba osób palących wynosi 20% ?

Nie zależnie od tego, który test wybierzemy procedura postępowania będzie wyglądać podobnie. Na początku naszym zadaniem będzie wyliczenie statystyki testowej. Następnie będziemy musieli z tablicy rozkładu chi kwadrat odczytać właściwą wartość.

Do odczytania właściwej wartości musimy znać ilość stopni swobody (df) oraz wartość założonego prawdopodobieństwa. Jeżeli znajdziemy już odpowiednią wartość pozostaje tylko porównać ją z wyliczona statystyką i na tej podstawie podjąć decyzję odnośnie odrzucenia lub nie odrzucenia założonej hipotezy.

Zapraszamy do zapoznania się z pozostałymi informacjami w naszej bazie wiedzy.

Jeśli potrzebujesz wsparcia w zakresie profesjonalnych analiz statystycznych do prac studenckich i naukowych to nie wahaj się nas zapytać o pomoc!